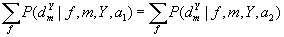I. INTRODUCTION
This essay is a reply to chapter 11 of the book authored by Mark Perakh entitled, Why Intelligent Design Fails: A Scientific Critique of the New Creationism (2004). The chapter can be review here. Chapter 11, “There is a Free Lunch After All: William Dembski’s Wrong Answers to Irrelevant Questions,” is a rebuttal to the book written by William Dembski entitled, No Free Lunch (2002). Mark Perakh’s also authored another anti-ID book, “Unintelligent Design.” The Discovery Institute replied to Perakh’s work here.
The book by William Dembski, No Free Lunch (2002) is a sequel to his classic, The Design Inference (1998). The Design Inference used mathematical theorems to define design in terms of a chance and statistical improbability. In The Design Inference, Dembski explains complexity, and demonstrated that when complex information is specified, it determines design. Simply put, Complex Specified Information (CSI) = design. It’s CSI that is the technical term that mathematicians, information theorists, and ID scientists can work with to determine whether some phenomenon or complex pattern is designed.
One of the most important contributors to ID Theory is American mathematician Claude Shannon, who is considered to be the father of Information Theory. Essentially, ID Theory is a sub-theory of Information Theory in the field of Bioinformatics. This is one of Dembski’s areas of expertise.
Claude Shannon is seen here with Theseus, his magnetic mouse. The mouse was designed to search through the corridors until it found the target.
Claude Shannon pioneered the foundations for modern Information Theory. His identifying units of information that can be quantified and applied in fields such as computer science is still called Shannon Information to this day.
Shannon invented a mouse that was programmed to navigate through a maze to search for a target, concepts that are integral to Dembski’s mathematical theorems of which are based upon Information Theory. Once the mouse solved the maze it could be placed anywhere it had been before and use its prior experience to go directly to the target. If placed in unfamiliar territory, the mouse would continue the search until it reached a known location and then proceed to the target. The ability of the device to add new knowledge to its memory is believed to be the first occurrence of artificial learning.
In 1950 Shannon published a paper on computer chess entitled Programming a Computer for Playing Chess. It describes how a machine or computer could be made to play a reasonable game of chess. His process for having the computer decide on which move to make is a minimax procedure, based on an evaluation function of a given chess position. Shannon gave a rough example of an evaluation function in which the value of the black position was subtracted from that of the white position. Material was counted according to the usual relative chess piece relative value. (http://en.wikipedia.org/wiki/Claude_Shannon).
Shannon’s work obviously involved applying what he knew at the time for the computer program to scan all possibilities for any given configuration on the chess board to determine the best optimum move to make. As you will see, this application of a search within any given phase space that might occur during the course of the game for a target, which is one fitness function among many as characterized in computer chess is exactly what the debate is about with Dembski’s No Free Lunch (NFL) Theorems.
When Robert Deyes wrote a review on Stephen Meyer’s “Signature In The Cell,” he noted “When talking about ‘information’ and its relevance to biological design, Intelligent Design theorists have a particular definition in mind.” Stephen Meyer explained in “Signature In The Cell” that information is: “the attribute inherent in and communicated by alternative sequences or arrangements of something that produce specific effects” (p.86).
When Shannon unveiled his theory for quantifying information it included several axioms, one of which is information is inversely proportional to uncertainty. Similarly, design can be contrasted to chance.
II. COMPLEX SPECIFIED INFORMATION (CSI):
CSI is based upon the theorem:
sp(E) and SP(E) ⟶ D(E)
When a small probably (SP) event (E) is complex, and
SP(E) = [P (E|I) < the Universal Probability Bound]. Or, in English, we know an event E is a small probably event when the probability of event E given I is less than the Universal Probability Bound. I = All relevant side information and all stochastic hypotheses. This is all in Dembski’s book, The Design Inference.
An event E is specified by a pattern independent of E, or expressed mathematically: sp(E). Upper case letters SP(E) are the small probability event we are attempting to determine is CSI, or designed. Lower case letters sp(E) are a prediction that we will discover the SP(E). Therefore, if sp(E) and SP(E) then ⟶ D(E). D(E) means the event E is not only small probability, but we can conclude it is designed.
Dembski’s Universal Probability Bound = 0.5 x 10-150, or 0.5 times 10 to the exponent negative 150 power. This is the magic number when one can scientifically be justified to invoke design. It’s been said that using Dembski’s formula, the probability that Dembski states must be matched in order to ascribe design is to announce in advance before dealing that you are going to be dealt 24 Royal Flushes in a row, and then the event plays out just exactly as the advance forecast. In other words, just as intelligence might be entirely illusory, so likewise CSI is nothing other than a mathematical ratio that might not have anything in the world to do with actual design.
The probability of dealing a Royal flush given all combinations of 5 cards randomly drawn from a full deck of 52 without replacement is 649,739 to 1. According to Dembski, if someone were to be dealt a Royal Flush 24 times in a row upon the advance announcement predicting such a happening would take place, his contentions would be that it was so improbable that someone cheated, or “design” would have had to been involved.
The probability of being dealt a Royal flush given all combinations of 5 cards randomly drawn from a full deck of 52 without replacement is 649,739 to 1.
I’m oversimplifying CSI just for the sake of making this point that we have already imposed upon the term “design” a technical definition that requires no intelligence or design as we understand the everyday normal use of the words. What’s important is that just as improbable as it is to be dealt a Royal Flush, so likewise the level of difficulty natural selection is up against to produce what appears to be designed in nature. And, when CSI is observed in nature, which occurs occasionally, then that not only confirms ID predictions, and defies Darwinian gradualism, but also tips a scientist a clue that such might be evidence of additional ID-related mechanisms at work.
It is true that William Dembski’s theorems are based upon an assumption that we can quantify everything in the universe; no argument there. But, he only used that logic to derive his Universal Probability Bound, which is nearly an infinitesimally small number: 0.5 x 10-150, or 0.5 times 10 to the exponent negative 150 power. Do you not think that when a probability is this low that it is a safe bet to invoke corruption of natural processes by an intelligent agency? The number is a useful number.
I wrote two essays on CSI to provide a better understanding of specified complexity introduced in Dembski’s book, The Design Inference. In this book, Dembski introduces and expands on the meaning of CSI, and then proceeds to present reasoning as to why CSI infers design. The first essay I wrote on CSI here is an elementary introduction to the overall concept. I wrote a second essay here that provides a more advances discussion on CSI.
CSI does show up in nature. That’s the whole point of the No Free Lunch Principle is that there is no way by which evolution can take credit for the occurrences when CSI shows up in nature.
III. NO FREE LUNCH
Basically, the book, “No Free Lunch” is a sequel to the earlier work, The Design Inference. While we get more calculations that confirm and verify Dembski’s earlier work, we also get new assertions made by Dembski. It is very important to note that ID Theory is based upon CSI that is established in The Design Inference. The main benefit of the second book, “No Free Lunch,” is that it further validates and verifies CSI, which was established in The Design Inference. The importance of this fact cannot be overemphasized. Additionally, “No Free Lunch” further confirms the validity of the assertion that design in inseparable from intelligence.
Before “No Free Lunch,” there was little effort demonstrating that CSI is connected to intelligence. That’s a problem because CSI = design. So, if CSI = design, it should be demonstrable that CSI correlates and is directly proportional to intelligence. This is the thesis of what the book, “No Free Lunch” sets out to do. If “No Free Lunch” fails to successfully support the thesis that CSI correlates to intelligence, that would not necessarily impair ID Theory, but if Dembski succeeds, then it would all the more lend credibility to ID Theory and certainly all of Dembski’s work as well.
IV. PERAKH’S ARGUMENT
The outline of Perakh’s critique of Dembski’s No Free Lunch theorems is as follows:
1. Methinks It Is like a Weasel—Again
2. Is Specified Complexity Smuggled into Evolutionary Algorithms?
3. Targetless Evolutionary Algorithms
4. The No Free Lunch Theorems
5. The NFL Theorems—Still with No Mathematics
6. The No Free Lunch Theorems—A Little Mathematics
7. The Displacement Problem
8. The Irrelevance of the NFL Theorems
9. The Displacement “Problem”
1. METHINKS IT IS LIKE A WEASEL – AGAIN
One common demonstration to help people understand how CSI works is to take a letter sequence. This can be done with anything, but the common example is this pattern:
METHINKS•IT•IS•LIKE•A•WEASEL
This letter arrangement is used the most often to describe CSI because the math has already been worked out. The bullets represent spaces. There are 27 possibilities at each location in a symbol string 28 characters in length. If natural selection were entirely random it would take 1 x 1040 (that’s 10 to the 40th exponent, or 1 with 40 zeroes to get to the decimal point). It’s a small probability. However, natural selection (NS) is smarter than that, and Richard Dawkins has shown how NS achieves similar odds in nature in an impressive 43 attempts to get the answer correct, as Dembski notes here.
In this example, the probability was only 1 x 1040. CSI is an even much more higher number than that. If you take a pattern or model, such as METHINKS•IT•IS•LIKE•A•WEASEL, and you keep adding the information, you soon reach probabilities that are within the domain of CSI.
Dembski’s explanation to the target sequence of METHINKS•IT•IS•LIKE•A•WEASEL is as follows:
“Thus, in place of 1040 tries on average for pure chance to produce the target sequence, by employing the Darwinian mechanism it now takes on average less than 100 tries to produce it. In short, a search effectively impossible for pure chance becomes eminently feasible for the Darwinian mechanism.
“So does Dawkins’s evolutionary algorithm demonstrate the power of the Darwinian mechanism to create biological information? No. Clearly, the algorithm was stacked to produce the outcome Dawkins was after. Indeed, because the algorithm was constantly gauging the degree of difference between the current sequence from the target sequence, the very thing that the algorithm was supposed to create (i.e., the target sequence METHINKS•IT•IS•LIKE•A•WEASEL) was in fact smuggled into the algorithm from the start. The Darwinian mechanism, if it is to possess the power to create biological information, cannot merely veil and then unveil existing information. Rather, it must create novel information from scratch. Clearly, Dawkins’s algorithm does nothing of the sort.
“Ironically, though Dawkins uses a targeted search to illustrate the power of the Darwinian mechanism, he denies that this mechanism, as it operates in biological evolution (and thus outside a computer simulation), constitutes a targeted search. Thus, after giving his METHINKS•IT•IS•LIKE•A•WEASEL illustration, he immediately adds: “Life isn’t like that. Evolution has no long-term goal. There is no long-distant target, no final perfection to serve as a criterion for selection.” [Footnote] Dawkins here fails to distinguish two equally valid and relevant ways of understanding targets: (i) targets as humanly constructed patterns that we arbitrarily impose on things in light of our needs and interests and (ii) targets as patterns that exist independently of us and therefore regardless of our needs and interests. In other words, targets can be extrinsic (i.e., imposed on things from outside) or intrinsic (i.e., inherent in things as such).
“In the field of evolutionary computing (to which Dawkins’s METHINKS•IT•IS•LIKE•A•WEASEL example belongs), targets are given extrinsically by programmers who attempt to solve problems of their choice and preference. Yet in biology, living forms have come about without our choice or preference. No human has imposed biological targets on nature. But the fact that things can be alive and functional in only certain ways and not in others indicates that nature sets her own targets. The targets of biology, we might say, are “natural kinds” (to borrow a term from philosophy). There are only so many ways that matter can be configured to be alive and, once alive, only so many ways it can be configured to serve different biological functions. Most of the ways open to evolution (chemical as well as biological evolution) are dead ends. Evolution may therefore be characterized as the search for alternative “live ends.” In other words, viability and functionality, by facilitating survival and reproduction, set the targets of evolutionary biology. Evolution, despite Dawkins’s denials, is therefore a targeted search after all.” (http://evoinfo.org/papers/ConsInfo_NoN.pdf).
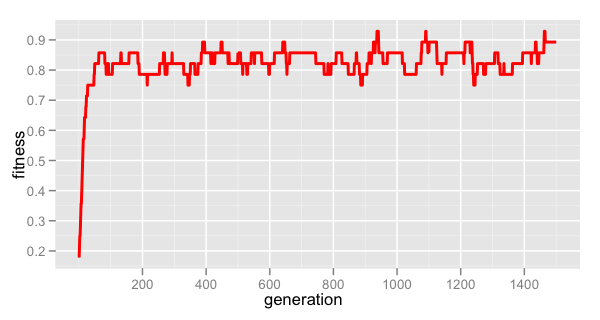
This graph was presented by a blogger who ran just one run of the weasel algorithm for Fitness of “best match” for n = 100 and u = 0.2.
Perakh doesn’t make any argument here, but introduces the METHINKS IT IS LIKE A WEASEL configuration here to be the initial focus of what is to follow. The only derogatory comment he makes with Dembski is to charge that Dembski is “inconsistent.” But, there’s no excuse to accuse Dembski of any contradiction. Perakh states himself, “Evolutionary algorithms may be both targeted and targetless” (Page 2). He also admits that Dembski was correct in that “Searching for a target IS teleological” (Page 2). Yet, Perakh blames Dembski to be at fault for simply noting the teleological inference, and falsely accuses Dembski of contradicting himself on this issue when there is no contradiction. There’s no excuse for Perakh to accuse Dembksi is being inconsistent here when all he did was acknowledge that teleology should be noted and taken into account when discussing the subject.
Perakh also states on page 3 that Dembski lamented over the observation made by Dawkins. This is unfounded rhetoric and ad hominem that does nothing to support Perakh’s claims. There is no basis to assert or benefit to gain by suggesting that Dembski was emotionally dismayed because of the observations made by Dawkins. The issue is a talking point for discussion.
Perakh correctly represents the fact, “While the meaningful sequence METHINKSITISLIKEAWEASEL is both complex and specified, a sequence NDEIRUABFDMOJHRINKE of the same length, which is gibberish, is complex but not specified” (page 4). And, then he correctly reasons the following,
“If, though, the target sequence is meaningless, then, according to the above quotation from Behe, it possesses no SC. If the target phrase possesses no SC, then obviously no SC had to be “smuggled” into the algorithm.” Hence, if we follow Dembski’s ideas consistently, we have to conclude that the same algorithm “smuggles” SC if the target is meaningful but does not smuggle it if the target is gibberish.” (Emphasis in original, page 4)
Perakh then arrives at the illogical conclusion that such reasoning is “preposterous because algorithms are indifferent to the distinction between meaningful and gibberish targets.” Perakh is correct that algorithms are indifferent to teleology and making distinctions. But, he has no basis to criticize Dembski on this point.
This 40-piece jigsaw puzzle is more complex than the Weasel problem that consists of only the letters M, E, T, H, I, N, K, S, L, A, W, S, plus a space.
In the Weasel problem submitted by Richard Dawkins, the solution (target) was provided to the computer up front. The solution to the puzzle was embedded in the letters provided to the computer to arrange into an intelligible sentence. The same analogy applies to a jigsaw puzzle. There is only one end result picture the puzzle pieces can be assembled to achieve. The information of the picture is embedded in the pieces and not lost from merely cutting the image picture into pieces. One can still solve the puzzle if they are blinded up front from seeing what the target looks like. There is only one solution to the Weasel problem, so it is a matter of deduction, and not a blind search as Perakh maintains. The task the Weasel algorithm had to perform was to unscramble the letters and rearrange them in the correct sequence.
The METHINKS•IT•IS•LIKE•A•WEASEL algorithm was given up front to be the fitness function, and intentionally designed CSI to begin with. It’s a matter of the definition of specified complexity (SC). If information is both complex and specified, then it is CSI by definition, and CSI = SC. They’re two ways to express the same identical concept. Perakh is correct. The algorithm has nothing in and of itself to do with the specified complexity of the target phrase. The reason why a target phrase is specified complexity is because the complex pattern was specified up front to be the target in the first place, all of which was independent of the algorithm. So, so far, Perakh has not made a point of argument yet.
Dembski makes subsequent comments about the weasel math here and here.
2. IS SPECIFIED COMPLEXITY SMUGGLED INTO EVOLUTIONARY ALGORITHMS?
Perakh asserts on page 4 that “Dembski’s modified algorithm is as teleological as Dawkins’s original algorithm.” So what? This is a pointless red herring that Perakh continues work for no benefit or support of any argument against Dembski. It’s essentially a non-argument. All sides: Dembski, Dawkins, and Perakh himself have conceded up front that discussion of this topic is difficult without stumbling over anthropomorphism. Dembski noted it up front, which is commendable; but somehow Perakh wrongfully tags this to be some fallacy of which Dembski is committing.
Personifying the algorithms to have teleological behavior was a fallacy noted up front. So, there’s no basis for Perakh to allege that Dembski is somehow misapplying any logic in his discussion. The point was acknowledged by all participants in the discussion from the very beginning. Perakh is not inserting anything new here, but just being an annoyance to raise a point that was already noted. Also, Perakh has yet to actually raise any actual argument yet.
Dembksi wrote in No Free Lunch (194–196) that evolutionary algorithms do not generate CSI, but can only “smuggle” it from a “higher order phase space.” CSI is also called specified complexity (SC). Perakh makes the ridiculous claim on page 4 that this point is irrelevant to biological evolution, but offers no reasoning as to why. To support his challenge against Dembski, Perakh states, “since biological evolution has no long-term target, it requires no injection of SC.”
The question is whether it’s possible a biological algorithm caused the existence of the CSI. Dembski says yes, and his theorems established in The Design Inference are enough to satisfy the claim. But, Perakh is arguing here that the genetic algorithm is capable of generating the CSI. Perakh states that natural selection is unaware of its result (page 4), which is true. Then he says Dembski must, “offer evidence that extraneous information must be injected into the natural selection algorithm apart from that supplied by the fitness functions that arise naturally in the biosphere.” Dembski shows this in “Life’s Conservation Law – Why Darwinian Evolution Cannot Create Biological Information.”
3. TARGETLESS EVOLUTIONARY ALGORITHMS
Biomorphs
Next, Perakh raises the example made by Richard Dawkins in “The Blind Watchmaker” in which Dawkins uses what he calls “biomorphs” as an argument against artificial selection. While Dawkins exhibits an imaginative jab to ridicule ID Theory, raising the subject again by Perakh is pointless. Dawkins used the illustration of biomorphs to contrast the difference between natural selection as opposed to artificial selection upon which ID Theory is based upon. It’s an excellent example. I commend Dawkins on coming up with these biomorph algorithms. They are very unique and original.
The biomorphs created by Dawkins are actually different intersecting lines of various degrees of complexity, and resemble Rorschach figures often used by psychologists and psychiatrists. Biomorphs depict both inanimate objects like a cradle and lamp, plus biological forms such as a scorpion, spider, and bat. It is an entire departure from evolution as it is impossible to make any logical connection how a fox would evolve into a lunar lander, or how a tree frog would morph into a precision balance scale. Since the idea is a departure from evolutionary logic of any kind, because no rationale to connect any of the forms is provided, it would be seemingly impossible to devise an algorithm that fits biomorphs.
Essentially, Dawkins used these biomorphs to propose a metaphysical conjecture. The intent of Dawkins is to suggest ID Theory is a metaphysical contemplation while natural selection is entirely logical reality. Dawkins explains the point in raising the idea of biomorphs is:
“… when we are prevented from making a journey in reality, the imagination is not a bad substitute. For those, like me, who are not mathematicians, the computer can be a powerful friend to the imagination. Like mathematics, it doesn’t only stretch the imagination. It also disciplines and controls it.”
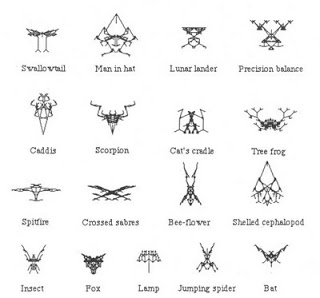
Biomorphs submitted by Richard Dawkins from The Blind Watchmaker, figure 5 p. 61
This is an excellent point and well-taken. The idea Dawkins had to reference biomorphs in the discussion was brilliant. Biomorphs are an excellent means to assist in helping someone distinguish the difference between natural selection verses artificial selection. This is exactly the same point design theorists make when protesting the personification of natural selection to achieve reality-defying accomplishments. What we can conclude is that scientists, regardless of whether they accept or reject ID Theory, dislike the invention of fiction to fill in unknown gaps of phenomena.
In the case of ID Theory, yes the theory of intelligent design is based upon artificial selection, just as Dawkins notes with his biomorphs. But, unlike biomorphs and the claim of Dawkins, ID Theory still is based upon fully natural scientific conjectures.
4. THE NO FREE LUNCH THEOREMS
In this section of the argument, Perakh doesn’t provide an argument. He’s more interested in talking about his hobby, which is mountain climbing.
The premise offered by Dembski that Perakh seeks to refute is the statement in No Free Lunch, which reads, “The No Free Lunch theorems show that for evolutionary algorithms to output CSI they had first to receive a prior input of CSI.” (No Free Lunch, page 223). Somehow, Perakh believes he can prove Dembski’s theorems false. In order to accomplish the task, one would have to analyze Dembski’s theorems. First of all, Dembski’s theorems take into account all the possible factors and variables that might apply, as opposed to the algorithms only. Perakh doesn’t make anything close to such an evaluation. Instead, Perakh does nothing but use the mountain climbing analogy to demonstrate we cannot know just exactly what algorithm natural selection will promote as opposed to which algorithms natural selection will overlook. This fact is a given up front and not in dispute. As such, Perakh presents a non-argument here that does nothing to challenge Dembski’s theorems in the slightest trace of a bit. Perakh doesn’t even discuss the theorems, let alone refute them.
The whole idea here of the No Free Lunch theorems is to demonstrate how CSI is smuggled across many generations, and then shows up visibly in a phenotype of a life form countless generations later. Many factors must be contemplated in this process including evolutionary algorithms. Dembksi’s book, No Free Lunch, is about demonstrating how CSI is smuggled through, which is the whole point as to where the book’s name is derived. If CSI is not manufactured by evolutionary processes, including genetic algorithms, then it had been displaced from the time it was initially front-loaded. Hence, there’s no free lunch.
Front-Loading could be achieved several ways, one of which is via panspermia.
But, Perakh makes no attempt to discuss the theorems in this section, much less refute Dembski’s work. I’ll discuss front-loading in the Conclusion.
5. THE NO FREE LUNCH THEOREMS—STILL WITH NO MATHEMATICS
Perakh finally makes a valid point here. He highlights a weakness in Dembski’s book that the calculations provided do little to account for an average performance of multiple algorithms in operation at the same time.
Referencing his mountain climbing analogy from the previous section, Perakh explains the fitness function is the height of peaks in a specific mountainous region. In his example he designates the target of the search to be a specific peak P of height 6,000 meters above sea level.
“In this case the number n of iterations required to reach the predefined height of 6,000 meters may be chosen as the performance measure. Then algorithm a1 performs better than algorithm a2 if a1 converges on the target in fewer steps than a2. If two algorithms generated the same sample after m iterations, then they would have found the target—peak P—after the same number n of iterations. The first NFL theorem tells us that the average probabilities of reaching peak P in m steps are the same for any two algorithms” (Emphasis in the original, page 10).
Since any two algorithms will have an equal average performance when all possible fitness landscapes are included, then the average number n of iterations required to locate the target is the same for any two algorithms if the averaging is done over all possible mountainous landscapes.
Therefore, Perakh concludes the no free lunch theorems of Dembski do not say anything about the relative performance of algorithms a2 and a1 on a specific landscape. On a specific landscape, either a2 or a1 may happen to be much better than its competitor. Perakh goes on to apply the same logic in a targetless context as well.
These points Perakh raises are well taken. Subsequent to the writing of Perakh’s book in 2004, Dembski ultimately provided the supplemental math to cure these issues in his paper entitled, “Searching Large Spaces: Displacement and the No Free Lunch Regress” (March 2005), which is available for review here. It should also be noted that Perakh concludes this section of chapter 11 by admitting that the No Free Lunch theorems “are certainly valid for evolutionary algorithms.” If that is so, then there is no dispute.
6. THE NO FREE LUNCH THEOREMS—A LITTLE MATHEMATICS
It is noted that Dembski’s first no free lunch theorem is correct. It is based upon any given algorithm performed m times. The result will be a time-ordered sample set d comprised of m measured values of f within the range Y. Let P be the conditional probability of having obtained a given sample after m iterations, for given f, Y, and m.
Then, the first equation is
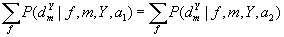when a1 or a2 are two different algorithms.
Perakh emphasizes this summation is performed over “all possible fitness functions.” In other words, Dembski’s first theorem proves that when algorithms are averaged over all possible fitness landscapes the results of a given search are the same for any pair of algorithms. This is the most basic of Dembski’s theorems, but the most limited for application purposes.
The second equation applies the first one for time-dependent landscapes. Perakh notes several difficulties in the no free lunch theorems including the fact that evolution is a “coevolutionary” process. In other words, Dembski’s theorems apply to ecosystems that involve a set of genomes all searching for the same fixed fitness function. But, Perakh argues that in the real biological world, the search space changes after each new generation. The genome of any given population slightly evolves from one generation to the next. Hence, the search space that the genomes are searching is modified with each new generation.
The game of Chess is played one successive procedural (evolutionary) step at a time. With each successive move (mutation) on the chessboard, the chess-playing algorithm must search for a different and new board configuration as to the next move the computer program (natural selection) should select for.
The no free lunch models discussed here are comparable to the computer chess game mentioned above. With each slight modification (Darwinian gradualism) in the step by step process of the chess game, the pieces end up in different locations on the chessboard so that the search process starts all over again with a new and different search for a new target than the preceding search.
There is one optimum move that is better than others, which might be a preferred target. Any other reasonable move on the chessboard is a fitness function. But, the problem in evolution is not as clear. Natural selection is not only blind, and therefore conducts a blind search, but does not know what the target should be either.
Where Perakh is leading to with this foundation is he is going to suggest in the next section that given a target up front, like the chess solving algorithm has, there might be enough information in the description of the target itself to assist the algorithm to succeed in at least locating a fitness function. Whether Perakh is correct or not can be tested by applying the math.
As aforementioned, subsequent to the publication of Perakh’s book, Dembski ultimately provided the supplemental math to cure these issues in his paper entitled, “Searching Large Spaces: Displacement and the No Free Lunch Regress” (March 2005), which is available for review here. It should also be noted that Perakh concludes this section of the chapter by admitting that the No Free Lunch theorem “are certainly valid for evolutionary algorithms.”
7. THE DISPLACEMENT PROBLEM
As already mentioned, the no free lunch theorems show that for evolutionary algorithms to output CSI they first received a prior input of CSI. There’s a term to describe this. It’s called displacement. Dembski wrote in a paper entitled “Evolution’s Logic of Credulity:
An Unfettered Response to Allen Orr” (2002) the key point of writing No Free Lunch concerns displacement. The “NFL theorems merely exemplify one instance not the general case.”
Dembski continues to explain displacement,
“The basic idea behind displacement is this: Suppose you need to search a space of possibilities. The space is so large and the possibilities individually so improbable that an exhaustive search is not feasible and a random search is highly unlikely to conclude the search successfully. As a consequence, you need some constraints on the search – some information to help guide the search to a solution (think of an Easter egg hunt where you either have to go it cold or where someone guides you by saying ‘warm’ and ‘warmer’). All such information that assists your search, however, resides in a search space of its own – an informational space. So the search of the original space gets displaced to a search of an informational space in which the crucial information that constrains the search of the original space resides” (Emphasis in the original, http://www.arn.org/docs/dembski/wd_logic_credulity.htm).
8. THE IRRELEVANCE OF THE NFL THEOREMS
In the conclusion of his paper, Searching Large Spaces: Displacement and the No Free Lunch Regress (2005), Dembski writes:
“To appreciate the significance of the No Free Lunch Regress in this latter sense, consider the case of evolutionary biology. Evolutionary biology holds that various (stochastic) evolutionary mechanisms operating in nature facilitate the formation of biological structures and functions. These include preeminently the Darwinian mechanism of natural selection and random variation, but also others (e.g., genetic drift, lateral gene transfer, and symbiogenesis). There is a growing debate whether the mechanisms currently proposed by evolutionary biology are adequate to account for biological structures and functions (see, for example, Depew and Weber 1995, Behe 1996, and Dembski and Ruse 2004). Suppose they are. Suppose the evolutionary searches taking place in the biological world are highly effective assisted searches qua stochastic mechanisms that successfully locate biological structures and functions. Regardless, that success says nothing about whether stochastic mechanisms are in turn responsible for bringing about those assisted searches.” (https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.330.8289&rep=rep1&type=pdf).
Up until this juncture, Perakh admits, “Within the scope of their legitimate interpretation—when the conditions assumed for their derivation hold—the NFL theorems certainly apply” to evolutionary algorithms. The only question so far in his critique up until this section was that he has argued the NFL theorems do not hold in the case of coevolution. However, subsequent to this critique, Dembski resolved those issues.
Here, Perakh reasons that even if the NFL theorems were valid for coevolution, he still rejects Dembski’s work because they are irrelevant. According to Perakh, if evolutionary algorithms can outperform random sampling, aka a “blind search,” then the NFL theorems are meaningless. Perakh bases this assertion on the statement by Dembski on page 212 of No Free Lunch, which provides, “The No Free Lunch theorems show that evolutionary algorithms, apart from careful fine-tuning by a programmer, are no better than blind search and thus no better than pure chance.”
Therefore, for Perakh, if evolutionary algorithms refute this comment by Dembski by outperforming a blind search, then this is evidence the algorithms are capable of generating CSI. If evolutionary algorithms generate CSI, then Dembski’s NFL theorems have been soundly falsified, along with ID Theory as well. If such were the case, then Perakh would be correct, the NFL theorems would indeed be irrelevant.
Perakh rejects the intelligent design “careful fine-tuning by a programmer” terminology in favor of just as reasonable of a premise:
“If, though, a programmer can design an evolutionary algorithm which is fine-tuned to ascend certain fitness landscapes, what can prohibit a naturally arising evolutionary algorithm to fit in with the kinds of landscape it faces?” (Page 19)
Perakh explains how his thesis can be illustrated:
“Naturally arising fitness landscapes will frequently have a central peak topping relatively smooth slopes. If a certain property of an organism, such as its size, affects the organism’s survivability, then there must be a single value of the size most favorable to the organism’s fitness. If the organism is either too small or too large, its survival is at risk. If there is an optimal size that ensures the highest fitness, then the relevant fitness landscape must contain a single peak of the highest fitness surrounded by relatively smooth slopes” (Page 20).
The graphs in Fig. 11.1 schematically illustrate Perakh’s thesis:
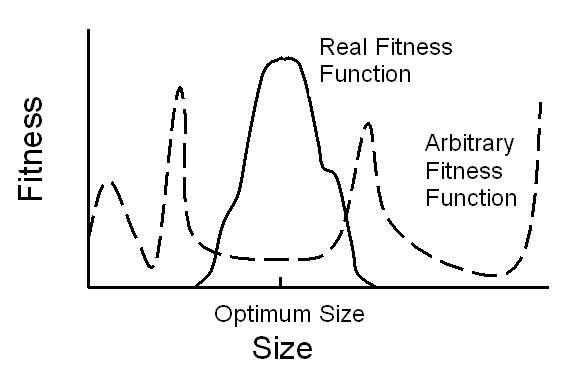
This is Figure 11.1 in Perakh’s book – Fitness as a function of some characteristic, in this case the size of an animal. Solid curve – the schematic presentation of a naturally arising fitness function, wherein the maximum fitness is achieved for a certain single-valued optimal animal’s size. Dashed curve – an imaginary rugged fitness function, which hardly can be encountered in the existing biosphere.
Subsequent to Perakh’s book published in 2004, Dembski did indeed resolve the issue raised here in his paper, “Conservation of Information in Search: Measuring the Cost of Success” (Sept. 2009), http://evoinfo.org/papers/2009_ConservationOfInformationInSearch.pdf. Dembski’s “Conservation of Information” paper starts with the foundation that there have been laws of information already discovered, and that idea’s such as Perakh’s thesis were falsified back in 1956 by Leon Brillouin, a pioneer in information theory. Brillouin wrote, “The [computing] machine does not create any new information, but it performs a very valuable transformation of known information” (L. Brillouin, Science and Information Theory. New York: Academic, 1956).
In his paper, “Conservation of Information,” Dembski and his coauthor, Robert Marks, go on to demonstrate how laws of conservation of information render evolutionary algorithms incapable of generating CSI as Perakh had hoped for. Throughout this chapter, Perakh continually cited the various works of information theorists, Wolpert and Macready. On page 1051 in “Conservation of Information” (2009), Dembski and Marks also quote Wolpert and Macready:
“The no free lunch theorem (NFLT) likewise establishes the need for specific information about the search target to improve the chances of a successful search. ‘[U]nless you can make prior assumptions about the . . . [problems] you are working on, then no search strategy, no matter how sophisticated, can be expected to perform better than any other.’ Search can be improved only by “incorporating problem-specific knowledge into the behavior of the [optimization or search] algorithm” (D. Wolpert and W. G. Macready, ‘No free lunch theorems for optimization,’ IEEE Trans. Evol. Comput., vol. 1, no. 1, pp. 67–82, Apr. 1997).”
In “Conservation of information” (2009), Dembski and Marks resoundingly demonstrate how conservation of information theorems indicate that even a moderately sized search requires problem-specific information to be successful. The paper proves that any search algorithm performs, on average, as well as random search without replacement unless it takes advantage of problem-specific information about the search target or the search-space structure.
Throughout “Conservation of information” (2009), the paper discusses evolutionary algorithms at length:
“Christensen and Oppacher note the ‘sometimes outrageous claims that had been made of specific optimization algorithms.’ Their concern is well founded. In computer simulations of evolutionary search, researchers often construct a complicated computational software environment and then evolve a group of agents in that environment. When subjected to rounds of selection and variation, the agents can demonstrate remarkable success at resolving the problem in question. Often, the claim is made, or implied, that the search algorithm deserves full credit for this remarkable success. Such claims, however, are often made as follows: 1) without numerically or analytically assessing the endogenous information that gauges the difficulty of the problem to be solved and 2) without acknowledging, much less estimating, the active information that is folded into the simulation for the search to reach a solution.” (Conservation of information, page 1058).
Dembski and Marks remind us that the concept Perakh is suggesting for evolutionary algorithms to outperform a blind search is the same scenario in the analogy of the proverbial monkeys typing on keyboards.
The monkeys at typewriters is a classic analogy to describe the chances of evolution being successful to achieve specified complexity.
A monkey at a typewriter is a good illustration for the viability of random evolutionary search. Dembski and Marks run the calcs for good measure using factors of 27 (26 letter alphabet plus a space) and a 28 character message. The answer is 1.59 × 1042, which is more than the mass of 800 million suns in grams.
In their Conclusion, Dembski and Marks state:
“Endogenous information represents the inherent difficulty of a search problem in relation to a random-search baseline. If any search algorithm is to perform better than random search, active information must be resident. If the active information is inaccurate (negative), the search can perform worse than random. Computers, despite their speed in performing queries, are thus, in the absence of active information, inadequate for resolving even moderately sized search problems. Accordingly, attempts to characterize evolutionary algorithms as creators of novel information are inappropriate.” (Conservation of information, page 1059).
9. THE DISPLACEMENT “PROBLEM”
This argument is based upon the claim by Dembski in page 202 of his book, “No Free Lunch, “ in which he states, “The significance of the NFL theorems is that an information-resource space J does not, and indeed cannot, privilege a target T.” However, Perakh highlights a problem with Dembski’s statement because the NFL theorems contain nothing about any arising ‘information-resource space.’ If Dembski wanted to introduce this concept within the framework of the NFL theorems, then he should have at least shown what the role of an “information-resource space” is in view of the “black-box” nature of the algorithms in question.
On page 203 of No Free Lunch, Dembski introduces the displacement problem:
“… the problem of finding a given target has been displaced to the new problem of finding the information j capable of locating that target. Our original problem was finding a certain target within phase space. Our new problem is finding a certain j within the information-resource space J.”
Perakh adds that the NFL theorems are indifferent to the presence or absence of a target in a search, which leaves the “displacement problem,” with its constant references to targets, hanging in the air.
Dembski’s response is as follows:
What is the significance of the Displacement Theorem? It is this. Blind search for small targets in large spaces is highly unlikely to succeed. For a search to succeed, it therefore needs to be an assisted search. Such a search, however, resides in a target of its own. And a blind search for this new target is even less likely to succeed than a blind search for the original target (the Displacement Theorem puts precise numbers to this). Of course, this new target can be successfully searched by replacing blind search with a new assisted search. But this new assisted search for this new target resides in a still higher-order search space, which is then subject to another blind search, more difficult than all those that preceded it, and in need of being replaced by still another assisted search. And so on. This regress, which I call the No Free Lunch Regress, is the upshot of this paper. It shows that stochastic mechanisms cannot explain the success of assisted searches.
“This last statement contains an intentional ambiguity. In one sense, stochastic mechanisms fully explain the success of assisted searches because these searches themselves constitute stochastic mechanisms that, with high probability, locate small targets in large search spaces. Yet, in another sense, for stochastic mechanisms to explain the success of assisted searches means that such mechanisms have to explain how those assisted searches, which are so effective at locating small targets in large spaces, themselves arose with high probability. It’s in this latter sense that the No Free Lunch Regress asserts that stochastic mechanisms cannot explain the success of assisted searches.” [Searching Large Spaces: Displacement and the No Free Lunch Regress (2005)].
Perakh makes some valid claims. About seven years later after the publication of Perakh’s book, Dembski provided updated calcs to the NFL theorems and his application of math to the displacement problem. This is available for review in his paper, “The Search for a Search: Measuring the Information Cost of Higher Level Search” (2010).
Perakh discusses the comments made by Dembski to support the assertion CSI must be necessarily “smuggled” or “front-loaded” into evolutionary algorithms. Perakh outright rejects Dembski’s claims, and proceeds to dismiss Dembski’s work on very weak grounds in what appears to be a hand-wave, begging the question as to how the CSI was generated in the first place, and overall circular reasoning.
Remember that the basis of the NFL theorems is to show that when CSI shows up in nature, it is only because it originated earlier in the evolutionary history of that population, and got smuggled into the genome of a population by regular evolution. The CSI might have been front-loaded millions of years earlier in the biological ancestry. The front-loading of the CSI may have occurred possibly in higher taxa. Regardless from where the CSI originated, the claim by Dembski is that the CSI appears visually now because it was inserted earlier because evolutionary processes do not generate CSI.
The smuggling forward of CSI in the genome is called displacement. The reason why the alleged law of nature called displacement occurs is because when applying Information Theory to identify CSI, the target of the search theorems is the CSI itself. Dembski explains,
“So the search of the original space gets displaced to a search of an informational space in which the crucial information that constrains the search of the original space resides. I then argue that this higher-order informational space (‘higher’ with respect to the original search space) is always at least as big and hard to search as the original space.” (Evolution’s Logic of Credulity: An Unfettered Response to Allen Orr, 2012.)
It is important to understand what Dembski means by displacement here because Perakh distorts displacement to mean something different in this section. Perakh asserts:
“An algorithm needs no information about the fitness function. That is how the ‘black-box’ algorithms start a search. To continue the search, an algorithm needs information from the fitness function. However, no search of the space of all possible fitness function is needed. In the course of a search, the algorithm extracts the necessary information from the landscape it is exploring. The fitness landscape is always given, and automatically supplies sufficient information to continue and to complete the search.” (Page 24)
To support these contentions, Perakh references Dawkins’s weasel algorithm for comparison. The weasel algorithm, says Perakh, “explores the available phrases and selects from them using the comparison of the intermediate phrases with the target.” Perakh then argues the fitness function has in the weasel example the built-in information necessary to perform the comparison. Perakh then concludes,
“This fitness function is given to the search algorithm; to provide this information to the algorithm, no search of a space of all possible fitness functions is needed and therefore is not performed.” (Emphasis in original, Page 24)
If Perakh is right, then the same is true for natural evolutionary algorithms. Having bought his own circular reasoning he then declares that his argument therefore renders Dembski’s “displacement problem” to be “a phantom.” (Page 24)
One of the problems with this argument is that Perakh admits that there is CSI, and offers no explanation as to how it originates and increases in the genome of a population that results in greater complexity. Perakh is begging the question. He offers no math, no algorithm, no calcs, no example. He merely imposes his own properties of displacement upon the application, which is a strawman argument, and then shoots down displacement. There’s no attempt to derive how the algorithm ever finds the target in the first place, which is disappointing given that Dembski provides the math to support his own claims.
Perakh appears to be convinced that evolutionary algorithmic searches taking place in the biological world are highly effective assisted searches that successfully locate target biological structures and functions. And, as such, he is satisfied that these evolutionary algorithms can generate CSI. What Perakh needs to remember is that a genuine evolutionary algorithm is still a stochastic mechanism. The hypothetical success of the evolutionary algorithm says nothing about whether stochastic mechanisms are in turn responsible for bringing about those assisted searches. Dembski explains,
“Evolving biological systems invariably reside in larger environments that subsume the search space in which those systems evolve. Moreover, these larger environments are capable of dramatically changing the probabilities associated with evolution as occurring in those search spaces. Take an evolving protein or an evolving strand of DNA. The search spaces for these are quite simple, comprising sequences that at each position select respectively from either twenty amino acids or four nucleotide bases. But these search spaces embed in incredibly complex cellular contexts. And the cells that supply these contexts themselves reside in still higher-level environments.” [Searching Large Spaces: Displacement and the No Free Lunch Regress (2005), pp. 31-32]
Dembski argues that the uniform probability on the search space almost never characterizes the system’s evolution, but instead it is a nonuniform probability that brings the search to a successful conclusion. The larger environment brings upon the scenario the nonuniform probability. Dembski notes that Richard Dawkins made the same point as Perakh in Climbing Mount Improbable (1996). In that book, Dawkins argued that biological structures that at first appearance seem impossible with respect to the uniform probability, blind search, pure randomness, etc., become probable when the probabilities are reset by evolutionary mechanisms.
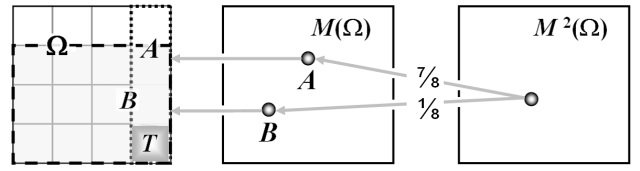
This diagram shows propagation of active information
through two levels of the probability hierarchy.
The kind of search Perakh presents is also addressed in “The Search for a Search: Measuring the Information Cost of Higher Level Search” (2010). The blind search Perakh complains of is that of uniform probability. In this kind of problem, given any probability measure on Ω, Dembski’s calcs indicate the active entropy for any partition with respect to a uniform probability baseline will be nonpositive (The Search for a Search, page 477). We have no information available about the search in Perakh’s example. All Perakh gives us is that the fitness function is providing the evolutionary algorithm clues so that the search is narrowed. But, we don’t know what that information is. Perakh’s just speculating that given enough attempts, the evolutionary algorithm will get lucky and outperform the blind search. Again, this describes uniform probability.
According to Dembski’s much intensified mathematical analysis, if no information about a search exists so that the underlying measure is uniform, which matches Perakh’s example, “then, on average, any other assumed measure will result in negative active information, thereby rendering the search performance worse than random search.” (The Search for a Search, page 477).
Dembski expands on the scenario:
“Presumably this nonuniform probability, which is defined over the search space in question, splinters off from richer probabilistic structures defined over the larger environment. We can, for instance, imagine the search space being embedded in the larger environment, and such richer probabilistic structures inducing a nonuniform probability (qua assisted search) on this search space, perhaps by conditioning on a subspace or by factorizing a product space. But, if the larger environment is capable of inducing such probabilities, what exactly are the structures of the larger environment that endow it with this capacity? Are any canonical probabilities defined over this larger environment (e.g., a uniform probability)? Do any of these higher level probabilities induce the nonuniform probability that characterizes effective search of the original search space? What stochastic mechanisms might induce such higher-level probabilities? For any interesting instances of biological evolution, we don’t know the answer to these questions. But suppose we could answer these questions. As soon as we could, the No Free Lunch Regress would kick in, applying to the larger environment once its probabilistic structure becomes evident.” [Searching Large Spaces: Displacement and the No Free Lunch Regress (2005), pp. 32]
The probabilistic structure would itself require explanation in terms of stochastic mechanisms. And, the No Free Lunch Regress blocks any ability to account for assisted searches in terms of stochastic mechanisms. See “Searching Large Spaces: Displacement and the No Free Lunch Regress” (2005).
Today, Dembski has updated his theorems to present by supplying additional math and contemplations. The NFL theorems today are analyzed in both a vertical and horizontal considerations in three-dimensional space.
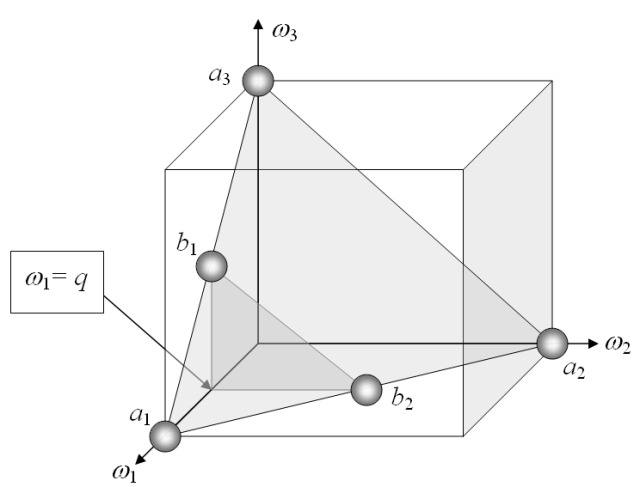
3-D Geometric Application of NFL Theorems
This diagram shows a three dimensional simplex in {ω1, ω2, ω3}. The numerical values of a1, a2 and a3 are one. The 3-D box in the figure presents two congruent triangles in a geometric approach to presenting a proof of the Strict Vertical No Free Lunch Theorem. In “The Search for a Search: Measuring the Information Cost of Higher Level Search” (2010), the NFL theorems are analyzed both horizontally and vertically. The Horizontal NFL Theorem pertains to showing the average relative performance of searches never exceeds unassisted or blind searches. The Vertical NFL Theorem shows that the difficulty of searching for a successful search increases exponentially with respect to the minimum allowable active information being sought.
This leads to the displacement principle, which holds that “the search for a good search is at least as difficult as a given search.” Perakh might have raised a good point, but Dembski’s done the math and confirmed his theorems are correct. Dembski’s math does work out, he’s provided the proofs, and shown the work. On the other hand, Perakh merely offered an argument that was nothing but an unverified speculation with no calcs to validate his point.
V. CONCLUSION
In the final section of this chapter, Perakh reiterates the main points throughout his article for review. He begins by saying,
“Dembski’s critique of Dawkins’s ‘targeted’ evolutionary algorithm fails to repudiate the illustrative value of Dawkins’s example, which demonstrates how supplementing random changes with a suitable law increases the rate of evolution by many orders of magnitude.” (Page 25)
No, this is a strawman. There was nothing Perakh submitted to establish such a conclusion. Neither Dembski or the Discovery Institute have any dispute with Darwinian mechanisms of evolution. The issue is whether ONLY such mechanisms are responsible for specified complexity (CSI). Intelligent Design proponents do not challenge that “supplementing random changes with a suitable law increases the rate of evolution by many orders of magnitude.”
Next, Perakh claims, “Dembski ignores Dawkins’s targetless’ evolutionary algorithm, which successfully illustrates spontaneous increase of complexity in an evolutionary process.” (Page 25).
No, this isn’t true. First, Dembski did not ignore the Dawkins’ weasel algorithm. Second, the weasel algorithm isn’t targetless. We’re given the target up front. We know exactly what it is. Third, the weasel algorithm did not show any increase in specified complexity. All the letters in the sequence already existed. When evolution operates in the real biological world, the genome of the population is reshuffled from one generation to the next. No new information is increasing leading to greater complexity. The morphology is a result from the same information being rearranged.
In the case of the Weasel example, the target was already embedded in the original problem, just like one and only one full picture is possible to assemble from pieces of a jigsaw puzzle. When the puzzle is completed, not one piece should be missing, unless one was lost, and there should not be one extra piece too many. The CSI was the original picture that was cut up into pieces to be reassembled. The Weasel example is actually a better illustration for front-loading. All the algorithm had to do was figure out how to arrange the letters back into the proper intelligible sequence.
The CSI was specified in the target or fitness function up front to begin with. The point of the NFL theorems indicates that if the weasel algorithm was a real life evolutionary example, then that complex specified information (CSI) would have been inputted into the genome of that population in advance. But, the analogy quickly breaks down for many reasons.
Perakh then falsely asserts, “Contrary to Dembski’s assertions, evolutionary algorithms routinely outperform a random search.” (Page 25). This is false. Perakh speculated that this was a possibility, and Dembski clearly not only refuted it, but demonstrated that evolutionary algorithms essentially never outperform a random search.
Perakh next maintains:
“Contrary to Dembski assertion, the NFL theorems do not make Darwinian evolution impossible. Dembski’s attempt to invoke the NFL theorems to prove otherwise ignores the fact that these theorems assert the equal performance of all algorithms only if averaged over all fitness functions.” (Page 25).
No, there’s no such assertion by Dembski. This is nonsense. Intelligent Design proponents do not assert any false dichotomy. ID Theory supplements evolution, providing the conjecture necessary to really explain the specified complexity. Darwinian evolution still occurs, but it only explains inheritance and diversity. It is ID Theory that explains complexity. As far as the NFL theorems asserting the equal performance of all or any algorithms to solve blind searches, this is ridiculous and never was established by Perakh.
Perakh also claims:
“Dembski’s constant references to targets when he discusses optimization searches are based on his misinterpretation of the NFL theorems, which entail no concept of a target. Moreover, his discourse is irrelevant to Darwinian evolution, which is a targetless process.” (Page 25).
No, Dembski did not misinterpret the very NFL theorems that he invented. The person that misunderstands and misrepresents them is Perakh. It is statements like this that cause one to suspect of Perakh understands what CSI might be, either. If you notice the trend in his writing, when Perakh looked for support for an argument, he referenced those who have authored rebuttals in opposition to Dembski’s work. But, when Perakh looked for an authority to explain the meaning of Dembski’s work, Perakh nearly always cited Dembski himself. Perakh never performs any math to support his own challenges. Finally, Perakh ever established anywhere that Dembski misunderstood or misapplied any of the principles of Information Theory.
Finally, Perakh ends the chapter with this gem:
“The arguments showing that the anthropic coincidences do not require the hypothesis of a supernatural intelligence also answer the questions about the compatibility of fitness functions and evolutionary algorithms.” (Page 25).
This is a strawman. ID Theory has nothing to do with the supernatural. If it did, then it would not be a scientific theory by definition of science, which is bases upon empiricism. As one can certainly see is obvious in this debate is that Intelligent Design theory is more aligned to Information Theory than most sciences. ID Theory is not about teleology, but is more about front-loading.
William Dembski’s work is based upon pitting “design” against chance. In his book, The Design Inference he used mathematical theorems and formulas to devise a definition for design based upon a mathematical probability. It’s an empirical way to work with improbable complex information patterns and sequences. It’s called specified complexity, or aka complex specified information (CSI). There’s no contemplation as to the source of the information other than it being front-loaded. ID Theory only involves a study of the information (CSI) itself. Design = CSI. We can study CSI because it is observable.
There is absolutely no speculation of any kind to suggest that the source of the information is by extraterrestrial beings or any other kind of designer, natural or non-natural. The study is only the information (CSI) itself — nothing else. There are several non-Darwinian conjectures as to how the information can develop without the need for designers. Other conjectures are panspermia, natural genetic engineering, and what’s called “front-loading.”
In ID, “design” does not require designers. It can be equated to be derived from “intelligence” as per William Dembski’s book, “No Free Lunch,” but he uses mathematics to support his work, not metaphysics. The intelligence could be illusory. All the theorems detect is extreme improbability because that’s all the math can do. And, it’s called “Complex Specified Information.” It’s the Information that ID Theory is about. There’s no speculation into the nature of the intelligent source, assuming that Dembski was right in determining the source is intelligent in the first place. All it takes really is nothing other than a transporter of the information, which could be an asteroid, which collides with Earth carrying complex DNA in the genome of some unicellular organism. You don’t need a designer to validate ID Theory; ID has nothing to do with designers except for engineers and intelligent agents that are actually observable.
Intelligent Design 
